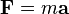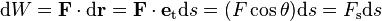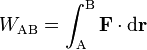Ley de gravitación universal.
La ley de gravitación universal es una ley física clásica que describe la interacción gravitatoria entre distintos cuerpos con masa.
Ésta fue presentada por Isaac Newton en su libro philosophoiac naturalis principia matemática,
publicado en 1687, donde establece por primera vez una relación
cuantitativa (deducida empíricamente de la observación) de la fuerza con
que se atraen dos objetos con masa. Así, Newton dedujo que la fuerza
con que se atraen dos cuerpos de diferente masa únicamente depende del
valor de sus masas y del cuadrado de la distancia que los separa. Para
grandes distancias de separación entre cuerpos se observa que dicha
fuerza actúa de manera muy aproximada como si toda la masa de cada uno
de los cuerpos estuviese concentrada únicamente en su centro de
gravedad, es decir, es como si dichos objetos fuesen únicamente un
punto, lo cual permite reducir enormemente la complejidad de las
interacciones entre cuerpos complejos.
Así, con todo esto resulta que la ley de la gravitación universal predice que la fuerza ejercida entre dos cuerpos de masas  y
y  separados una distancia
separados una distancia  es proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia, es decir:
es proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia, es decir:
 y
y  separados una distancia
separados una distancia  es proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia, es decir:
es proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia, es decir:
donde
 es el módulo de la fuerza ejercida entre ambos cuerpos, y su dirección se encuentra en el eje que une ambos cuerpos.
es el módulo de la fuerza ejercida entre ambos cuerpos, y su dirección se encuentra en el eje que une ambos cuerpos. es la constante de gravitación universal.
es la constante de gravitación universal.
Es decir, cuanto más masivos sean los cuerpos y más cercanos se encuentren, con mayor fuerza se atraerán.
El valor de esta constante de Gravitación Universal no pudo ser
establecido por Newton, que únicamente dedujo la forma de la interacción
gravitatoria, pero no tenía suficientes datos como para establecer
cuantitativamente su valor. Únicamente dedujo que su valor debería ser
muy pequeño. Sólo mucho tiempo después se desarrollaron las técnicas
necesarias para calcular su valor, y aún hoy es una de las constantes
universales conocidas con menor precisión. En 1798 se hizo el primer intento de medición(véase el experimento de Cavendish) y en la actualidad, con técnicas mucho más precisas se ha llegado a estos resultados:
En unidades del Sistema Internacional.
Esta ley recuerda mucho a la forma de la ley de Coulomb para las fuerzas electrostáticas, ya que ambas leyes siguen una ley de la inversa del cuadrado
(es decir, la fuerza decae con el cuadrado de la distancia) y ambas son
proporcionales al producto de magnitudes propias de los cuerpos (en el
caso gravitatorio de sus masas y en el caso electrostático de su carga
eléctrica).
Leyes de Newton.
 |
| AUTOR:RONANGEL ARTIGAS |
En concreto, la relevancia de estas leyes radica en dos aspectos:
- Por un lado, constituyen, junto con la transformación de Galileo, la base de la mecánica clásica.
- Por otro, al combinar estas leyes con la ley de la gravitación universal, se pueden deducir y explicar las leyes de Kepler sobre el movimiento planetario.
Así, las leyes de Newton permiten explicar tanto el movimiento de los astros, como los movimientos de los proyectiles artificiales creados por el ser humano, así como toda la mecánica de funcionamiento de las máquinas.
 |
| autor: lisi valderrama |
La dinámica de Newton, también llamada dinámica clásica, sólo se cumple en los sistemas de referencia inerciales (que se mueven a velocidad constante; la Tierra, aunque gire y rote, se trata como tal a efectos de muchos experimentos prácticos).
Solo es aplicable a cuerpos cuya velocidad dista considerablemente de la velocidad de la luz (que no se acerquen a los 300 000 km/s); la razón estriba en que cuanto más cerca esté un cuerpo de alcanzar esa velocidad (lo que ocurriría en los sistemas de referencia no-inerciales), más posibilidades hay de que incidan sobre el mismo una serie de fenómenos denominados efectos relativistas o fuerzas ficticias, que añaden términos suplementarios capaces de explicar el movimiento de un sistema cerrado de partículas clásicas que interactúan entre sí. El estudio de estos efectos (aumento de la masa y contracción de la longitud, fundamentalmente) corresponde a la teoría de la relatividad especial, enunciada por Albert Einstein en 1905.
Fundamentos de las leyes.
 |
| AUTOR:GÉNESIS VALERA |
Newton no asume
que la cantidad
de movimiento
es el resultado del producto de la masa por la velocidad, y define
dos tipos de fuerzas:
la vis insita,
que es proporcional a la masa y que refleja la inercia
de la materia, y la vis
impressa
(momento de
fuerza), que es la acción que cambia el estado de un cuerpo, sea
cual sea ese estado; la vis
impressa,
además de producirse por choque o presión, puede deberse a la vis
centrípeta
(fuerza
centrípeta), una fuerza que lleva al cuerpo hacia algún punto
determinado.
A diferencia de
las otras causas, que son acciones de contacto, la vis
centrípeta es
una acción
a distancia. En esta distingue Newton tres tipos de cantidades de
fuerza: una absoluta, otra aceleradora y, finalmente, la motora, que
es la que interviene en la ley fundamental del movimiento.
En tercer lugar,
precisa la importancia de distinguir entre lo absoluto y relativo
siempre que se hable de tiempo, espacio, lugar o movimiento.
En este sentido,
Newton, que entiende el movimiento como una traslación de un cuerpo
de un lugar a otro, para llegar al movimiento absoluto y verdadero de
un cuerpo.
las leyes de Newton.
Primera ley de Newton o ley de la inercia
La primera ley del movimiento rebate la idea aristotélica de que un
cuerpo solo puede mantenerse en movimiento si se le aplica una fuerza. Newton expone que:
Todo cuerpo persevera en su estado de reposo o movimiento uniforme
y rectilíneo a no ser que sea obligado a cambiar su estado por
fuerzas impresas sobre él.
 |
| AUTOR:OSWAR FLORES |
Esta ley postula, por tanto, que un cuerpo no puede cambiar por sí solo su estado inicial, ya sea en reposo o en movimiento rectilíneo uniforme,
a menos que se aplique una fuerza o una serie de fuerzas cuyo
resultante no sea nulo sobre él.
Newton toma en cuenta, así, el que los
cuerpos en movimiento están sometidos constantemente a fuerzas de roce o
fricción, que los frena de forma progresiva, algo novedoso respecto de
concepciones anteriores que entendían que el movimiento o la detención
de un cuerpo se debía exclusivamente a si se ejercía sobre ellos una
fuerza, pero nunca entendiendo como esta a la fricción.
En consecuencia, un cuerpo con movimiento rectilíneo uniforme implica
que no existe ninguna fuerza externa neta o, dicho de otra forma; un
objeto en movimiento no se detiene de forma natural si no se aplica una
fuerza sobre él. En el caso de los cuerpos en reposo, se entiende que su
velocidad es cero, por lo que si esta cambia es porque sobre ese cuerpo
se ha ejercido una fuerza neta.
La primera ley de Newton sirve para definir un tipo especial de
sistemas de referencia conocidos como Sistemas de referencia inerciales,
que son aquellos sistemas de referencia desde los que se observa que un
cuerpo sobre el que no actúa ninguna fuerza neta se mueve con velocidad
constante.
Segunda ley de Newton o ley de fuerza.
La segunda ley del movimiento de Newton dice:
El cambio de movimiento es proporcional a la fuerza motriz impresa y ocurre según la línea recta a lo largo de la cual aquella fuerza se imprime.
 |
| autor:lizzie nuñez |
En la mayoría de las ocasiones hay más de una fuerza actuando sobre
un objeto, en este caso es necesario determinar una sola fuerza
equivalente ya que de ésta depende la aceleración resultante. Dicha
fuerza equivalente se determina al sumar todas las fuerzas que actúan
sobre el objeto y se le da el nombre de fuerza neta.7
En términos matemáticos esta ley se expresa mediante la relación:
Donde:
 es el momento lineal
es el momento lineal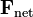 la fuerza total o fuerza resultante.
la fuerza total o fuerza resultante.
Suponiendo que la masa es constante y que la velocidad es muy inferior a la velocidad de la luzb la ecuación anterior se puede reescribir de la siguiente manera:
Sabemos que  es el momento lineal, que se puede escribir m.V donde m es la masa del cuerpo y V su velocidad.
es el momento lineal, que se puede escribir m.V donde m es la masa del cuerpo y V su velocidad.
 es el momento lineal, que se puede escribir m.V donde m es la masa del cuerpo y V su velocidad.
es el momento lineal, que se puede escribir m.V donde m es la masa del cuerpo y V su velocidad.
Consideramos a la masa constante y podemos escribir  aplicando estas modificaciones a la ecuación anterior:
aplicando estas modificaciones a la ecuación anterior:
 aplicando estas modificaciones a la ecuación anterior:
aplicando estas modificaciones a la ecuación anterior: |
| AUTOR: RONANGEL ARTIGAS |
La fuerza es el producto de la masa por la aceleración, que es la ecuación fundamental de la dinámica, donde la constante de proporcionalidad, distinta para cada cuerpo, es su masa de inercia. Veamos lo siguiente, si despejamos m de la ecuación anterior obtenemos que m es la relación que existe entre  y
y  .
Es decir la relación que hay entre la fuerza aplicada al cuerpo y la
aceleración obtenida. Cuando un cuerpo tiene una gran resistencia a
cambiar su aceleración (una gran masa) se dice que tiene mucha inercia.
Es por esta razón por la que la masa se define como una medida de la
inercia del cuerpo.
.
Es decir la relación que hay entre la fuerza aplicada al cuerpo y la
aceleración obtenida. Cuando un cuerpo tiene una gran resistencia a
cambiar su aceleración (una gran masa) se dice que tiene mucha inercia.
Es por esta razón por la que la masa se define como una medida de la
inercia del cuerpo.
 y
y  .
Es decir la relación que hay entre la fuerza aplicada al cuerpo y la
aceleración obtenida. Cuando un cuerpo tiene una gran resistencia a
cambiar su aceleración (una gran masa) se dice que tiene mucha inercia.
Es por esta razón por la que la masa se define como una medida de la
inercia del cuerpo.
.
Es decir la relación que hay entre la fuerza aplicada al cuerpo y la
aceleración obtenida. Cuando un cuerpo tiene una gran resistencia a
cambiar su aceleración (una gran masa) se dice que tiene mucha inercia.
Es por esta razón por la que la masa se define como una medida de la
inercia del cuerpo.
Por tanto, si la fuerza resultante que actúa sobre una partícula no
es cero, esta partícula tendrá una aceleración proporcional a la
magnitud de la resultante y en dirección de ésta. La expresión anterior
así establecida es válida tanto para la mecánica clásica como para la mecánica relativista,
a pesar de que la definición de momento lineal es diferente en las dos
teorías: mientras que la dinámica clásica afirma que la masa de un
cuerpo es siempre la misma, con independencia de la velocidad con la que
se mueve, la mecánica relativista establece que la masa de un cuerpo
aumenta al crecer la velocidad con la que se mueve dicho cuerpo.
De la ecuación fundamental se deriva también la definición de la unidad de fuerza o newton
(N). Si la masa y la aceleración valen 1, la fuerza también valdrá 1;
así, pues, el newton es la fuerza que aplicada a una masa de un
kilogramo le produce una aceleración de 1 m/s². Se entiende que la
aceleración y la fuerza han de tener la misma dirección y sentido.
La importancia de esa ecuación estriba sobre todo en que resuelve el
problema de la dinámica de determinar la clase de fuerza que se necesita
para producir los diferentes tipos de movimiento: rectilíneo uniforme (m.r.u), circular uniforme (m.c.u) y uniformemente acelerado (m.r.u.a).
Si sobre el cuerpo actúan muchas fuerzas, habría que determinar
primero el vector suma de todas esas fuerzas. Por último, si se tratase
de un objeto que cayese hacia la tierra con una resistencia del aire
igual a cero, la fuerza sería su peso, que provocaría una aceleración
descendente igual a la de la gravedad.
autores del vídeo : Roy Perez , Ronangel A , Igdamaris M , Lisi V(voz) , Cristhofer B(edición)
Tercera ley de Newton o principio de acción y reacción
la tercera ley de movimiento de Newton expresa que:
Con toda acción ocurre siempre una reacción igual y contraria: quiere decir que las acciones mutuas de dos cuerpos siempre son iguales y dirigidas en sentido opuesto.
La tercera ley de Newton es completamente original (pues las dos
primeras ya habían sido propuestas de otras maneras por Galileo,
Hooke y
Huygens)
y hace de las leyes de la mecánica un conjunto lógico y completo.8
Expone que por cada fuerza que actúa sobre un cuerpo (empuje),
este realiza una fuerza de igual intensidad, pero de sentido
contrario sobre el cuerpo que la produjo. Dicho de otra forma, las
fuerzas, situadas sobre la misma recta, siempre se presentan en pares
de igual magnitud y de dirección, pero con sentido opuesto.
 |
| autor: igdamaris moscan |
Es importante observar que este principio relaciona dos fuerzas
que no están aplicadas al mismo cuerpo, produciendo en ellos
aceleraciones diferentes, según sean sus masas. Por lo demás, cada
una de esas fuerzas obedece por separado a la segunda ley. Junto con
las anteriores leyes, ésta permite enunciar los principios de
conservación
del momento
lineal y del momento
angular.
trabajo y energía.
trabajo:
En mecánica clásica, se dice que una fuerza realiza trabajo cuando altera el estado de movimiento de un cuerpo. El trabajo de la fuerza sobre ese cuerpo será equivalente a la energía necesaria para desplazarlo de manera acelerada. El trabajo es una magnitud física escalar que se representa con la letra 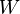 (del inglés Work) y se expresa en unidades de energía, esto es en julios o joules (J) en el Sistema Internacional de Unidades.
(del inglés Work) y se expresa en unidades de energía, esto es en julios o joules (J) en el Sistema Internacional de Unidades.
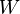 (del inglés Work) y se expresa en unidades de energía, esto es en julios o joules (J) en el Sistema Internacional de Unidades.
(del inglés Work) y se expresa en unidades de energía, esto es en julios o joules (J) en el Sistema Internacional de Unidades.
Ya que por definición el trabajo es un tránsito de energía, nunca se refiere a él como incremento de trabajo, ni se simboliza como ΔW. y esta sedivide en tres tipo:
El trabajo en mecánica.
Trabajo de una fuerza. Consideremos una partícula  sobre la que actúa una fuerza
sobre la que actúa una fuerza  , función de la posición de la partícula en el espacio, esto es
, función de la posición de la partícula en el espacio, esto es  y sea
y sea  un desplazamiento elemental (infinitesimal) experimentado por la partícula durante un intervalo de tiempo
un desplazamiento elemental (infinitesimal) experimentado por la partícula durante un intervalo de tiempo  . Llamamos trabajo elemental,
. Llamamos trabajo elemental,  , de la fuerza
, de la fuerza  durante el desplazamiento elemental
durante el desplazamiento elemental  al producto escalar
al producto escalar  ; esto es,
; esto es,
 sobre la que actúa una fuerza
sobre la que actúa una fuerza  , función de la posición de la partícula en el espacio, esto es
, función de la posición de la partícula en el espacio, esto es  y sea
y sea  un desplazamiento elemental (infinitesimal) experimentado por la partícula durante un intervalo de tiempo
un desplazamiento elemental (infinitesimal) experimentado por la partícula durante un intervalo de tiempo  . Llamamos trabajo elemental,
. Llamamos trabajo elemental,  , de la fuerza
, de la fuerza  durante el desplazamiento elemental
durante el desplazamiento elemental  al producto escalar
al producto escalar  ; esto es,
; esto es,
 |
| autor:ronangel artigas |
 Si representamos por
Si representamos por  la longitud de arco (medido sobre la trayectoria de la partícula) en el desplazamiento elemental, esto es
la longitud de arco (medido sobre la trayectoria de la partícula) en el desplazamiento elemental, esto es  , entonces el vector tangente a la trayectoria viene dado por
, entonces el vector tangente a la trayectoria viene dado por 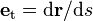 y podemos escribir la expresión anterior en la forma
y podemos escribir la expresión anterior en la forma
donde  representa el ángulo determinado por los vectores
representa el ángulo determinado por los vectores 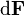 y
y  y
y 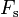 es la componente de la fuerza F en la dirección del desplazamiento elemental
es la componente de la fuerza F en la dirección del desplazamiento elemental  .
.
 representa el ángulo determinado por los vectores
representa el ángulo determinado por los vectores 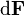 y
y  y
y 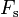 es la componente de la fuerza F en la dirección del desplazamiento elemental
es la componente de la fuerza F en la dirección del desplazamiento elemental  .
.
El trabajo realizado por la fuerza  durante un desplazamiento elemental de la partícula sobre la que está
aplicada es una magnitud escalar, que podrá ser positiva, nula o
negativa, según que el ángulo
durante un desplazamiento elemental de la partícula sobre la que está
aplicada es una magnitud escalar, que podrá ser positiva, nula o
negativa, según que el ángulo  sea agudo, recto u obtuso.
sea agudo, recto u obtuso.
 durante un desplazamiento elemental de la partícula sobre la que está
aplicada es una magnitud escalar, que podrá ser positiva, nula o
negativa, según que el ángulo
durante un desplazamiento elemental de la partícula sobre la que está
aplicada es una magnitud escalar, que podrá ser positiva, nula o
negativa, según que el ángulo  sea agudo, recto u obtuso.
sea agudo, recto u obtuso.
Si la partícula P recorre una cierta trayectoria en el espacio, su
desplazamiento total entre dos posiciones A y B puede considerarse como
el resultado de sumar infinitos desplazamientos elementales  y el trabajo total realizado por la fuerza
y el trabajo total realizado por la fuerza  en ese desplazamiento será la suma de todos esos trabajos elementales; o sea
en ese desplazamiento será la suma de todos esos trabajos elementales; o sea
 y el trabajo total realizado por la fuerza
y el trabajo total realizado por la fuerza  en ese desplazamiento será la suma de todos esos trabajos elementales; o sea
en ese desplazamiento será la suma de todos esos trabajos elementales; o sea
Esto es, el trabajo viene dado por la integral curvilínea de  a lo largo de la curva
a lo largo de la curva  que une los dos puntos; en otras palabras, por la circulación de
que une los dos puntos; en otras palabras, por la circulación de  sobre la curva
sobre la curva  entre los puntos A y B. Así pues, el trabajo es una magnitud física
escalar que dependerá en general de la trayectoria que una los puntos A y
B, a no ser que la fuerza
entre los puntos A y B. Así pues, el trabajo es una magnitud física
escalar que dependerá en general de la trayectoria que una los puntos A y
B, a no ser que la fuerza  sea conservativa,
en cuyo caso el trabajo resultará ser independiente del camino seguido
para ir del punto A al punto B, siendo nulo en una trayectoria cerrada.
Así, podemos afirmar que el trabajo no es una variable de estado.
sea conservativa,
en cuyo caso el trabajo resultará ser independiente del camino seguido
para ir del punto A al punto B, siendo nulo en una trayectoria cerrada.
Así, podemos afirmar que el trabajo no es una variable de estado.
 a lo largo de la curva
a lo largo de la curva  que une los dos puntos; en otras palabras, por la circulación de
que une los dos puntos; en otras palabras, por la circulación de  sobre la curva
sobre la curva  entre los puntos A y B. Así pues, el trabajo es una magnitud física
escalar que dependerá en general de la trayectoria que una los puntos A y
B, a no ser que la fuerza
entre los puntos A y B. Así pues, el trabajo es una magnitud física
escalar que dependerá en general de la trayectoria que una los puntos A y
B, a no ser que la fuerza  sea conservativa,
en cuyo caso el trabajo resultará ser independiente del camino seguido
para ir del punto A al punto B, siendo nulo en una trayectoria cerrada.
Así, podemos afirmar que el trabajo no es una variable de estado.
sea conservativa,
en cuyo caso el trabajo resultará ser independiente del camino seguido
para ir del punto A al punto B, siendo nulo en una trayectoria cerrada.
Así, podemos afirmar que el trabajo no es una variable de estado.Trabajo y energía cinética.
Para el caso de una partícula tanto en mecánica clásica como en mecánica relativista es válida la siguiente expresión:
Multiplicando esta expresión escalarmente por la velocidad e
integrando respecto al tiempo se obtiene que el trabajo realizado sobre
una partícula (clásica o relativista) iguala a la variación de energía cinética:
Trabajo y energía cinética
Para el caso de una partícula tanto en mecánica clásica como en mecánica relativista es válida la siguiente expresión:
Multiplicando esta expresión escalarmente por la velocidad e
integrando respecto al tiempo se obtiene que el trabajo realizado sobre
una partícula (clásica o relativista) iguala a la variación de energía cinética:

energía.
En física, «energía» se define como la capacidad para realizar un trabajo. En tecnología y economía, «energía» se refiere a un recurso natural (incluyendo a su tecnología asociada) para extraerla, transformarla y darle un uso industrial o económico.
 |
| autor: roy perez |

Transformación de la energía.
Para la optimización de recursos y la adaptación a nuestros usos,
necesitamos transformar unas formas de energía en otras. Todas ellas se
pueden transformar en otra cumpliendo los siguientes principios
termodinámicos:
- “La energía no se crea ni se destruye; solo se transforma”. De este modo, la cantidad de energía inicial es igual a la final.

- “La energía se degrada continuamente hacia una forma de energía de menor calidad (energía térmica)”. Dicho de otro modo, ninguna transformación se realiza con un 100 % de rendimiento, ya que siempre se producen unas pérdidas de energía térmica no recuperable. El rendimiento de un sistema energético es la relación entre la energía obtenida y la que suministramos al sistema.
Unidades de medida de energía.
La unidad de energía definida por el Sistema Internacional de Unidades es el julio, que se define como el trabajo realizado por una fuerza de un newton en un desplazamiento de un metro en la dirección de la fuerza, es decir, equivale a multiplicar un Newton por un metro. Existen muchas otras unidades de energía, algunas de ellas en desuso.